
已知直三棱柱ABC-A1B1C1.中,侧面AA1B1B为正方形, AB= BC = 2, E, F分别为AC和CC1的中点,D为棱A1B1上的点,BF丄A1B1.
(1) 证明:BF⊥DE;
⑵ 当为B1D何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?
答案
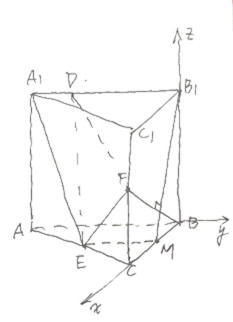
(1)直棱柱ABC-A1B1C1,侧面AA1B1B为正方形
所以A1B1=B1B=AB=BC=2
所以侧面BB1C1C为正方形
取BC中点M,连接B1M和EM
因为F为CC1重点,所以B1M⊥BF
由已知BF⊥A1B1
且A1B1B1M=B1
所以BF⊥平面A1B1M
由于E为AC中点,所以EM∥A1B1
所以EM平面A1B1M,所以BF⊥DE
(2)由(1)可知,A1B1⊥BF,且A1B1⊥B1B,所以A1B1⊥平面B1BCC1
以B为原点,BC,BY,BB1为xyz轴建立空间直角坐标系
设C(2,0,0),A(0,-2,0),B1(0,0,2)
C1(2,0,2),A1(0,-2,2),E(1,-1,0),F(2,0,1),D(0,n,2)
则向量EF=(1,1,1),向量FD=(-2,n,1)